DETERMINAN MATRIKS - PENGERTIAN, SIFAT - SIFAT, DAN CONTOH SOAL

 DETERMINAN MATRIKS 

A. Pengertian dan Definisi Determinan

Di dalam bidang materi al jabar linear, determinan adalah suatu bilangan real yang diperoleh dari suatu proses dengan aturan tertentu terhadap matriks bujur sangkar.

Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau | A |. Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.

Determinan Matriks Ordo 2 x 2

Matriks ordo 2 dinyatakan dalam bentuk matriks dengan jumlah kolom dan baris sama dengan dua. Nilai determinan A disimbolkan dengan | A |, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.

 
Soal: Tentukan nilai determinan matriks berikut.

  

Pembahasan:

determinan matriks A:
| A | = ad – bc
= 3 × 5 – 1 × 2
= 15 – 2
= 13

 Determinan Matriks Ordo 3 x 3

Matriks Ordo 3 adalah matriks persegi dengan banyaknya kolom dan baris sama dengan tiga. Misalnya pada matriks A, elemen-elemen pada baris pertama adalah a b c, baris kedua adalah d e f, dan baris ketiga adalah g h i. Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus seperti terlihat pada gambar di bawah.

 
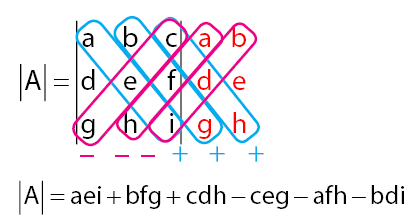
Contoh perhitungan determinan pada matriks ordo 3:

  

Maka determinan matriks A adalah,

  

  

  

  

B. Sifat-Sifat Determinan

1. Jika setiap elemen suatu baris atau kolom dari suatu matriks bujur sangkar A bernilai nol, maka det (A) = 0.

2. Jika A adalah suatu matriks bujur sangkar, maka det (A) = det (A ^T).

3. Jika setiap elemen dari suatu baris atau kolom pada determinan dari matriks A dikalikan dengan suatu skalar k, maka k bisa dikeluarkan dari tanda determinan, atau : det(kA) = k.det(A).

4. Jika matriks B diperoleh dari matriks A dengan cara mempertukarkan dua baris atau dua kolom, maka det(B) = - det(A).

5. Jika dua baris atau kolom matriks A identik, maka det(A) = 0 Dua matriks dikatakan identik , jika suatu baris merupakan hasil kali dengan skalar k (di mana k anggota bilangan real) dari baris yang lain, atau suatu kolom merupakan hasil kali dengan skalar k ( di mana k anggota bilangan real) dari kolom yang lain.

6. Jika A dan B dua matriks bujur sangkar yang mempunyai ukuran sama, maka det(AB) = det(A) det(B).

C. Cara Menentukan Nilai Determinan

Matriks berordo 2 x 2
Matriks berordo 3 x 3
Matriks berordo n x n
Dengan matriks kofaktor
Dengan Transformasi Baris Elementer (TBE)

1. Menentukan nilai determinan matriks berordo 2 x 2

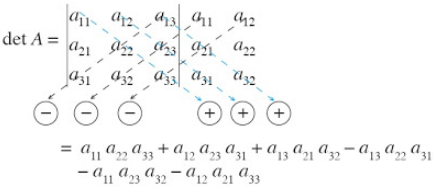
2. Menentukan nilai determinan matriks berordo 3 x 3 dengan Aturan Sarrus

3. Menentukan determinan matriks n x n dengan matriks Kofaktor

• a. Minor dari suatu matriks bujur sangkar A adalah harga determinan sub matriks yang tetap, setelah menghilangkan baris ke i dan kolom ke j. Minor dari baris ke i dan kolom ke j, dinotasikan dengan M_ij.
• b. Kofaktor dari suatu matriks bujur sangkar dilambangkan dengan cij, yaitu c_ij = (-1)^i+j M_ij

Ada 2 cara, yaitu :

1. Ekspansi Kofaktor sepanjang baris ke i : det(A) = a_i1c_i1 + a_i2c_i2 + … + a_inc_in
2. Ekspansi Kofaktor sepanjang kolom ke j : det(A) = a_1jc_1j + a_2jc_2j + … + a_njc_nj

4. Menentukan determinan matriks n x n dengan Transformasi Baris Elementer (TBE)

• a. Menukarkan dua baris Notasi = b_ij Arti = menukarkan baris ke-i dgn baris ke-j
• b. Mengalikan suatu bari dengan skalar k, k ≠ 0 Notasi = k.b_i Arti = mengalikan setiap elemen dari baris ke- i, dengan skalar k, k ≠ 0
• c. Menambahkan baris ke- i dengan k kali baris ke- j (k ≠ 0) Notasi= b_ij(k) Arti = b_i + k b_j (Perubahan terjadi pada b_i).

5. Menentukan Determinan Matriks dengan TBE Langkah :

• a. Dengan menggunakan TBE, ubahlah matriks yang ada, menjadi Matriks Segitiga Atas / Bawah.
• b. Harga determinannya adalah perkalian antar elemen–elemen pada diagonal utamanya.

D. Contoh Soal Determinan Ordo 2×2

• Hitunglah dan Tentukan berapa nilai determinan dari sebuah matrik berikut :Pembahasan:

  M=

  5 2 4 3

  Jawab :

  det(M) =

  5 2 4 3

  Maka = (5 × 3) – (2 × 4) = 7

Determinan Matriks Ordo 3×3

• Contohnya yang kita ketahui ialah pada sebuah matriks A, yang menjadi matriks persegi dengan ordo dua.

  Maka :A=

  A b C d

  Dengan demikian, dapat diperoleh sebuah rumus det A sebagai berikut:

  det(A) =

  A b C d

  Maka = ad – bc

  Contoh :

  Hitunglah dan Tentukan berapa nilai determinan dari matrik berikut :M=

  5 6 4 3

  Pembahasan:

  det(M) =

  5 6 4 3

  = (5 × 3) – (6 × 4) = 16

Determinan Matriks Ordo 3×3

• Ada dua cara dalam menghitung determinan untuk matriks berordo 3×3, yakni:

  • Metode Sarrus
  • Metode Minor-Kofaktor

  Cara yang paling mudah atau yang paling sering digunakan dalam menghitung suatu determinan matriks untuk yang berordo 3×3 adalah metode sarrus.

Metode Sarrus

• Contohnya anda memiliki matriks A dengan ordo 3×3 seperti berikut :

  A =

  a11         a12         a13

  a21         a22         a23

  a31         a32         a33

  Maka cara menghitung determinannya bisa ditunjukkan dengan gambar sebagai berikut :

  

  Contoh :

  Berikut ini tentukanlah nilai dari Determinan matriks ordo 3×3 berikut :A =

  2 3 4 5 4 3 7   1

  Pembahasan:

  Nilai determinan untuk matriks di atas ialah sebagai berikut:

  det(A) =

  2 3 4 5 4 3 7   1

  2 3 5 4 7

  det(A) = 2.4.1 + 3.3.7 + 4.5. – 4.4.7 – 2.3. – 3.5.1
  = 8 +63 + -112 – – 15
  = – 56